Chapitre 9 : Produit matriciel de carrés magiques
9.1 Introduction
Nous avons vu comment additionner deux carrés magiques et nous savons que le résultat de cette addition est encore un carré magique. De même, un carré magique multiplié par un nombre k est toujours un carré magique. Mais qu’en est-il du produit, au sens matriciel, de deux carrés magiques?
Connaissant ce produit, il est surprenant de voir les résultats inattendus qui vont suivre. Nous connaissons beaucoup d’exemples où le produit de deux carrés magiques n’est pas un carré magique mais aussi, des exemples où le produit de deux carrés magiques est un carré magique. De même, qu’en est-il de la puissance entière positive d’un carré magique? Si, par exemple, A est un carré magique d’ordre 3, alors que pouvons-nous dire de A affecté de la puissance 323 456 549 877? Avons-nous toujours un carré magique? Nous verrons, un peu plus loin, que ce carré sera bien magique!
9.2 Produit matriciel de carrés magiques
Rappelons qu’un carré est semi-magique si la somme des nombres de chaque rangée et de chaque colonne est toujours égale à un même nombre S et que le produit de deux carrés d’ordre n est un carré d’ordre n. Voyons maintenant ce magnifique résultat :
Théorème 9.1 :

Nous pouvons donc affirmer que si A et B sont des carrés magiques de sommes S et T , alors le produit AB est au moins un carré semi-magique de somme ST .
Puis, si A est un carré semi-magique de somme S , alors Ak est un carré semi-magique de somme Sk où k est un entier ≥ 1.
Preuve du théorème :
Les éléments de A sont aij, ses rangées sont Ai; les éléments de B sont bij, ses colonnes sont Bj; les éléments de C = AB sont cij.
Trouvons la somme des éléments de la rangée i de AB :
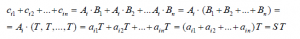
La somme des éléments de chaque rangée de AB est donc ST.
Trouvons maintenant la somme des éléments de la colonne j de AB :

La somme des éléments de chaque colonne de AB est donc ST. Ainsi, le produit AB est un carré semi-magique de somme ST .
Nous savons maintenant que le produit de deux carrés magiques d’ordre n de sommes S et T est au moins un carré semi-magique de somme ST . Mais quand le produit est-il magique?
Théorème 9.2 :

Preuve :
Soit C , le carré magique trivial d’ordre n formé que du nombre 1. Nous pouvons donc écrire :
\(A = \begin{pmatrix} \frac{S}{n} \end{pmatrix}C\) et \(B = \begin{pmatrix} \frac{T}{n} \end{pmatrix}C\). Puis \(AB = \begin{pmatrix} \frac{ST}{n^2} \end{pmatrix}C^2 = \begin{pmatrix} \frac{ST}{n^2} \end{pmatrix}nC = \begin{pmatrix} \frac{ST}{n} \end{pmatrix}C\).
Donc le produit AB est un carré magique trivial de somme ST car chaque nombre dans ce carré égale \(\frac{ST}{n}\).
Nous avons AB = BA (Voir le problème 5 de 9.6)
[…]
