Chapitre 8 : Des carrés magiques spectaculaires
8.1 Introduction
Nous venons de définir, au chapitre précédent, les carrés ultra-magiques et hyper-magiques sans pour autant montrer comment les construire.
Un carré ultra-magique non trivial d’ordre 3 n’existe pas. En effet, celui-ci est associatif (problème 9 de 7.4) mais n’est pas pandiagonal (problème 8 de 7.4).
Les ultra-magiques d’ordre 4 non triviaux existent mais aucun n’est normal et même, aucun n’est presque normal. Pour montrer cela, nous partons de la structure générale des carrés magiques pandiagonaux d’ordre 4 qui est exactement la même que celle des super-Dürer d’ordre 4, (voir section 5.5) lesquels sont des Dürer. Si nous rendons associative cette structure,
nous trouvons :
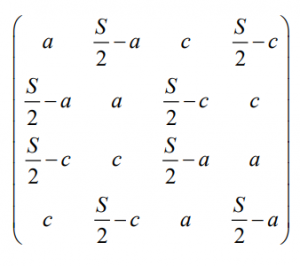
La section 5.9 nous montre comment rendre associatif un Dürer. C’est ce que nous avons fait pour avoir la structure ci-haut.
Un ultra-magique d’ordre 4 a obligatoirement cette forme. Il est clair que ce carré magique n’est ni normal, ni presque normal. Nous avons au mieux quatre nombres différents, chacun apparaissant quatre fois.
Pour les ultra-magiques d’ordre 5, la section 6.3 nous présente une structure générale laquelle permet de trouver les 128 ultra-magiques normaux d’ordre 5 qui existent. Tous les ultra-magiques d’ordre 5 ont en commun 362 figures magiques.
Pour les ultra-magiques d’ordres supérieurs à 5, le travail sera plus ardu. Il faudra partir de la structure générale et imposer sur celle-ci les conditions nécessaires pour avoir la structure des carrés magiques à la fois associatifs et pandiagonaux. Cette structure renfermera un nombre de variables qui augmentera avec l’ordre du carré. De là la grande difficulté lorsque nous partons de la structure générale. Comment trouver la structure des ultra-magiques d’ordre 2500? Pouvons-nous y arriver par d’autres moyens?
Quant aux hyper-magiques, la difficulté est la même lorsque nous voulons les construire et en particulier, lorsque l’ordre du carré est très grand.
Nous allons construire dans les deux sections suivantes, deux carrés magiques d’ordre 8 dont l’un sera un hyper-magique. Pour ce faire, nous partirons de la structure générale des carrés magiques d’ordre 8, laquelle renferme 48 variables.
Les cases du premier carré d’ordre 8 que nous allons construire ici sont numérotées de gauche à droite et de haut en bas avec les entiers de 1 à 64 :
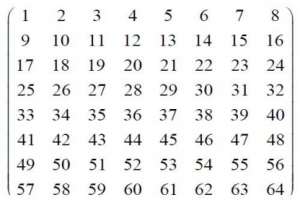
Nous définissons un petit carré d’ordre 2 contenu dans le grand carré à l’aide des numéros qui identifient les quatre cases du petit carré. Par exemples : nous pouvons parler du carré (1 ; 2 ; 9 ; 10), (2 ; 3 ; 10 ; 11), (10 ; 11 ; 18 ; 19), (37 ; 38 ; 45 ; 46), … Il y en a en tout 49.
Nous voulons que la somme des quatre cases de chaque carré d’ordre 2 soit égale à 4S/n. Pour ce faire, nous allons additionner les expressions situées dans chaque carré d’ordre 2. Nous commencerons avec le carré (1 ; 2 ; 9 ; 10) et nous poserons la somme des expressions des quatre cases égale à 4S/n = S/2. De cette équation, nous allons isoler une variable et la remplacer dans la structure générale G des carrés magiques d’ordre 8, par son expression.
Nous obtiendrons alors une nouvelle structure générale G1 qui renfermera 47 variables. Cette nouvelle structure générale donnera tous les carrés magiques d’ordre 8 avec la somme des cases du carré (1 ; 2 ; 9 ; 10) égale à S/2. Nous allons continuer jusqu’à ce que les 49 carrés d’ordre 2 aient pour somme S/2. Le nombre de variables aura considérablement diminué lorsque nous atteindrons notre dernière nouvelle structure générale.
[….]
