Chapitre 6 : Les carrés magiques d’ordre 5
6.1 Introduction
Nous allons faire une petite excursion dans l’espace vectoriel E5 des carrés magiques d’ordre 5. Cet espace vectoriel est de dimension n ( n – 2) = 15. En construisant la structure générale de E5, nous trouverons donc un carré magique général dans lequel il y aura quinze variables libres. Nous allons trouver trois sous-espaces qui contiendront des carrés magiques remarquables. Par exemple, les Ariane, qui possèdent onze fusées, forment un sous-espace de dimension 4. Puis, les ultra-magiques qui sont pandiagonaux et associatifs, forment un sous-espace de dimension 5. Enfin, le sous-espace des ultra-magiques-alpha, de dimension 3. Nous verrons ces trois sous-espaces un peu plus loin.
Précisons qu’un carré magique d’ordre n et de somme S est associatif si chaque fois que nous prenons deux nombres situés dans deux cases en positions symétriques par rapport au centre du carré, la somme de ceux-ci est toujours \(\frac{2S}{n}\).
Les A-Dürer, que nous avons vus au chapitre précédent, sont tous associatifs; en fait, ce sont des Dürer associatifs.
Les carrés magiques normaux d’ordre 5 sont de somme magique S = 65 et f(65) = 1394. Nous retrouvons donc 1394 figures magiques dans tous les carrés magiques normaux d’ordre 5. De plus, le nombre de carrés magiques normaux primitifs d’ordre 5 est très grand soit:
275 305 224
Pour les 4×4, nous n’en avions que 880 et pour les 3×3, 1 seul!!!
Nous savons qu’un carré magique d’ordre 3 et de somme S a obligatoirement comme centre le nombre \(\frac{S}{3}\). S’il est normal, son centre est 5. Pour les carrés magiques d’ordre 5, le centre est-il toujours \(\frac{S}{5}\)? Le centre est-il toujours 13 si le carré est normal? La réponse est non et pour illustrer cela, voici vingt-cinq carrés magiques pandiagonaux normaux d’ordre 5. Ils renferment respectivement comme centre les entiers de 1 à 25. Ils sont donc tous primitifs. Ils ont été
construits en appliquant une petite règle sur un premier carré normal pandiagonal et celui-ci seul nous a permis de trouver les vingt-quatre autres. Voici cette règle appelée 1-3-5-2-4 :
- Choisissons A, un carré magique pandiagonal.
- Ses rangées, de haut en bas, sont notées 1, 2, 3, 4 et 5.
- Construisons le carré B en plaçant de haut en bas, les rangées 1, 3, 5, 2 et 4 de A.
- Les colonnes de B, de gauche à droite, sont notées 1, 2, 3, 4 et 5.
- Construisons le carré C en plaçant de gauche à droite, les colonnes 1, 3, 5, 2 et 4 de B.
- Le carré C ainsi obtenu est magique et pandiagonal. L’élément de A qui occupe la position (5 ; 5) est maintenant l’élément central de C.
- Si en plus, A est normal, alors, évidemment, C le sera aussi.
De la même façon, nous avons la règle 1-3-5-7-2-4-6 pour les carrés magiques
pandiagonaux d’ordre 7. Le résultat est encore un carré magique pandiagonal et l’élément en position (7 ; 7) dans A devient le centre de C. Suivent les vingt-cinq pandiagonaux normaux 5×5 de centres de 1 à 25; le nombre en-dessous de chaque carré de centre k indique le nombre de carrés magiques normaux parmi les 275 305 224 qui ont le nombre k comme centre; ceci en fait une très belle classification :
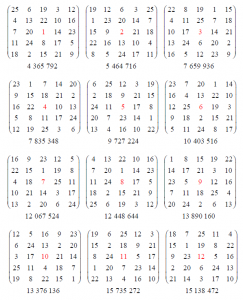
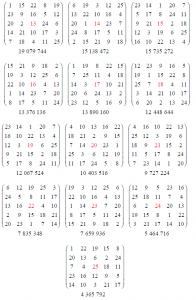
Donc, le centre d’un carré magique d’ordre 5 n’est pas obligatoirement le nombre \(\frac{S}{5}\).
[…]
