Chapitre 15 : Les carrés multiplicatifs
15.1 Introduction
Considérons un carré d’ordre n tel que le produit des nombres de chaque rangée, chaque colonne et chaque grande diagonale soit toujours égal à un même nombre P appelé produit magique. Un tel carré se nomme carré multiplicatif.

Si un carré multiplicatif d’ordre n ≥ 3 est presque normal, alors son produit magique est non nul. Il en est de même si les n² nombres d’un carré multiplicatif sont différents deux à deux, le produit sera toujours non nul. En effet, dans ce cas, si le carré contient le nombre 0, alors il n’en contient qu’un seul et ce carré ne pourra pas être multiplicatif.

Ces carrés multiplicatifs existent pour tous les ordres n ≥ 1. Pour n = 1, l’unique case contient un seul nombre.
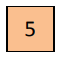
Ici, rangée, colonne et diagonales se confondent et le produit magique est P = 5.
Pour n = 2, il est facile de montrer que le carré a une des formes suivantes :

Le carré de droite renferme trois zéros et m est un nombre réel quelconque. Mais ces carrés ne sont pas presque normaux! (Voir problème 1 de 15.7)
Pour n ≥ 3, nous pouvons utiliser l’exponentiation pour construire une infinité de carrés multiplicatifs à partir d’un seul carré magique, lequel existe toujours.
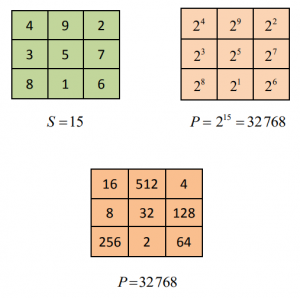
D’où le carré multiplicatif de produit magique P =32768. Ici, l’exponentiation était en base a = 2.
Nous aurions pu choisir une toute autre base et ainsi remplacer x dans le carré magique par \(3^x\) ou \(4^x\) ou \(5^x\), …
Par contre, ce procédé d’exponentiation nous donne des carrés multiplicatifs qui renferment de très grands nombres. Que dire si la base était 60 ou 34567? Cependant, nous verrons plus loin que tout carré multiplicatif formé de nombres positifs (>0) s’obtient par exponentiation!!!
Notons que dans le procédé d’exponentiation, tous les nombres du carré multiplicatif ont la forme \(a^m\) où m est un nombre du carré magique et a > 0, un nombre réel fixe.
Si A et B sont deux carrés magiques différents d’ordre n ≥ 3, alors il est évident que les deux carrés multiplicatifs obtenus par exponentiation de base 0 < a < 1 ou a > 1, seront différents.
De plus, si M est un carré magique d’ordre n et N, le carré multiplicatif obtenu par exponentiation, alors M et N possèdent exactement les mêmes figures magiques. Une figure magique dans un carré magique d’ordre n et de somme S est un groupe de n cases distinctes de somme S tandis qu’une figure magique dans un carré multiplicatif d’ordre n et de produit P est un groupe de
n cases distinctes de produit P.
[…]
