Chapitre 13 : Les carrés magiques de Christian Boyer
13.1 Introduction
Christian Boyer est né en France, près de Bordeaux, en mai 1958. Il est ingénieur, informaticien et mathématicien. Parmi ses centres d’intérêts, mentionnons les nombres premiers, les algorithmes de factorisation et les mathématiques récréatives, en particulier, les carrés, cubes et hyper-cubes magiques.
Ses carrés et cubes magiques sont extraordinaires et d’une grande beauté!!! Nous allons les voir sous peu mais avant, parlons de multi-magie, de carrés multiplicatifs et de carrés additifs multiplicatifs.
Soit A, un carré magique d’ordre n. Si, dans chaque case, nous élevons au carré le nombre qui s’y trouve, alors nous obtenons un nouveau carré. Celui-ci, en général, n’est pas magique mais quand il l’est, nous disons alors que A est un carré bi-magique.
Si nous mettons au carré chaque nombre d’un carré magique A et que le carré qui en résulte est encore magique et si en plus, nous mettons au cube chaque nombre de A et que le carré qui en résulte est toujours magique, alors nous disons que A est un carré tri-magique.

Un carré bi-magique est donc un carré 2-multi-magique et un carré tri-magique est un carré 3-multi-magique.
Voyons maintenant un autre type de carrés : les carrés multiplicatifs. La multiplication remplace ici l’addition.

13.2 Les carrés k-multi-magiques
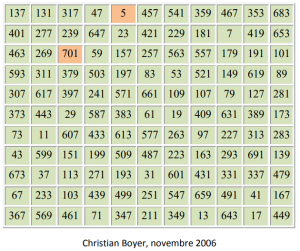
Voici un objet mathématique exceptionnel; c’est un carré bi-magique d’ordre 11 formé de 121 nombres premiers consécutifs allant de 5 à 701, en excluant 523, 641 et 677. Il est donc formé de 121 nombres premiers choisis parmi les 126 premiers nombres premiers. Les deux sommes magiques sont : S1 = 3 497 et S2 = 1 578 251.
C’est le premier carré bi-magique formé exclusivement de nombres premiers tous différents. Il a été construit par Christian Boyer en novembre 2006. Le voici :
En mai 2001, Christian Boyer et André Viricel ont construit un carré tétra-magique (4-multi-magique) d’ordre 512; il renferme 262 144 entiers consécutifs allant de 0 à 262 143. Pour le rendre normal, il suffit d’ajouter 1 à chaque nombre du carré et le nouveau carré sera toujours tétra-magique (voir le théorème 13.2). Dans le carré normal, nous trouverons aux extrémités de
la première rangée, le plus petit et le plus grand entier du carré et sur la dernière rangée, à l’extrémité droite, nous trouverons l’ordre 512 du carré.
[…]
