Chapitre 2 : Opérations sur les carrés magiques, espaces vectoriels
Nous pouvons regarder les carrés magiques comme des matrices carrées. Certains parlent même de matrices magiques.
L’addition de deux carrés magiques de même ordre se fait exactement comme l’addition de deux matrices carrées de même taille.
La multiplication d’un carré magique par un nombre réel (un scalaire) se fait de la même façon qu’avec une matrice.
Dans le but de simplifier, nous allons souvent représenter un carré magique par une matrice.
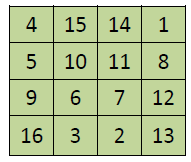
Ainsi, le carré magique ci-haut peut prendre la forme matricielle suivante :
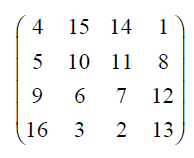
Voyons un exemple d’addition de carrés magiques et de multiplication d’un carré magique par un nombre mais avant, rappelons que nous notons souvent un élément d’une matrice A par aij qui n’est rien d’autre que l’élément situé à l’intersection de la i-ème rangée et de la j-ème colonne. Si nous appelons B, le carré précédent, alors l’élément b23 est le nombre 11 et l’élément b42 est le nombre 3.

Pour faire A + B, nous additionnons les nombres qui occupent les mêmes positions dans chaque carré. L’élément cij dans A + B s’obtient donc comme suit : cij = aij + bij.
Pour faire 5B, nous devons multiplier chaque nombre de B par 5. L’élément cij de 5B est donné par cij = 5bij et d’une façon générale, l’élément cij de k B s’écrit cij = k bij .
Il est clair que si A et B sont des carrés magiques respectivement de sommes S et T, alors A + B est un carré magique de somme S + T et k A est un carré magique de somme k S. De plus, les propriétés des opérations sur les matrices s’appliquent aux carrés magiques d’où le théorème 2.1 qui suit. Nous pouvons aussi faire le produit (matriciel) de deux carrés magiques A et B. Ce produit AB, en général, n’est pas un carré magique. Nous verrons dans le chapitre 9 le théorème qui affirme que si A et B sont des carrés magiques respectivement de sommes S et T, alors le produit AB est un carré semi-magique de somme ST. Nous verrons aussi que les puissances impaires de certains carrés magiques sont encore des carrés magiques!
Soient M un carré magique d’ordre n et W, le carré trivial d’ordre n qui renferme l’entier 1 dans toutes ses cases. Ajouter le nombre k dans toutes les cases de M revient à faire M + k W qui est toujours un carré magique. Nous pourrons écrire M + k au lieu de M + kW.
[…]
