Chapitre 12 : Les carrés magiques fonctionnels
12.1 Introduction
Nous avons jusqu’à maintenant toujours considéré les carrés magiques formés de nombres réels et plus particulièrement formés d’entiers. Cependant, un carré magique peut aussi être formé de nombres complexes, de nombres qui appartiennent à un corps (commutatif) quelconque, d’objets qui appartiennent à un anneau unitaire commutatif.
Ces objets pourraient être des polynômes ou en général, des fonctions. Nous parlerons alors de carrés magiques fonctionnels ou simplement de carrés fonctionnels.
12.2 Quelques exemples
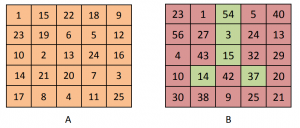
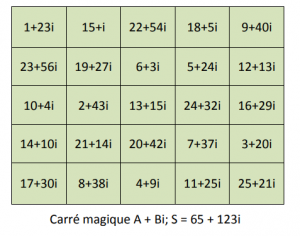
Les carrés A et B sont magiques de sommes 65 et 123. Le carré A + Bi est formé de 25 nombres complexes; il est magique de somme 65 + 123 i.
Le carré suivant est un carré magique formé de neuf polynômes du troisième degré. Sa somme magique est le polynôme 9x³ – 12x² – 3x. C’est un carré fonctionnel.
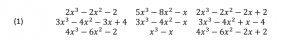
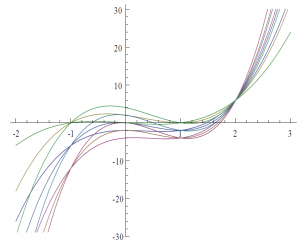
Les neuf courbes représentatives sont illustrées ci-dessous :
Si dans le carré magique (1), nous donnons à x une valeur réelle, alors nous obtenons un carré magique formé de neuf nombres. Avec x = 3, nous trouvons le carré magique suivant de somme 9x³ – 12x² – 3x évalué à x = 3, soit 126.
\(\begin{pmatrix} 34 & 60 & 32 \\ 40 & 42 & 44 \\ 52 & 24 & 50 \end{pmatrix}\)
Il est très intéressant de voir comment les courbes représentatives des neuf polynômes se rencontrent. D’abord, nous pouvons observer que les neuf courbes se rencontrent au point (2; 6). Nous appelons nœud un tel point. À x = –1 et à x =1, les neuf courbes se rencontrent par groupes de trois. Nous pouvons créer de telles intersections à volonté!!! Nous verrons comment un peu plus loin. En général, il est possible de trouver l’intervalle dans lequel auront lieu toutes les intersections et il est possible d’identifier à l’avance tous les types d’intersections possibles.
[…]
