Chapitre 11 : Les carrés arithmétiques
11.1 Introduction
Considérons l’espace vectoriel sur le corps des nombres réels, des carrés magiques d’ordre n. La structure générale qui représente cet espace renferme n (n – 2) variables libres et pour construire un tel carré magique, il nous faut attribuer une valeur réelle à chacune de ces variables. Pour n = 12, par exemple, nous avons 120 variables libres (dont la somme S). Si nous voulons construire un carré magique formé de 144 entiers positifs différents, le travail ne sera pas simple. D’abord, il nous faut trouver 120 entiers positifs différents et les attribuer aux 120 variables. Les autres entiers seront déterminés par des expressions linéaires (à coefficients entiers) renfermant des variables parmi les 120. De plus, nous n’avons que très peu de contrôle sur ces nouveaux entiers. Certains peuvent être négatifs et il peut y avoir des répétitions. Il n’y a pas de problème à faire disparaitre les entiers négatifs mais pendant que nous faisons disparaitre une répétition, d’autres peuvent apparaitre ailleurs. Si nous désirons un carré magique normal d’ordre 12, le travail sera encore plus compliqué.
Bien entendu, nous pouvons utiliser des méthodes connues depuis longtemps et celles-ci nous permettront d’en obtenir un. Mais en trouver à partir de la structure générale des carrés magiques d’ordre 12 est un peu inquiétant!
Vous nous demandez de construire un carré magique normal d’ordre 12 et 200 carrés magiques presque normaux (formés de 144 entiers positifs différents) d’ordre 12. Votre commande est énorme!!! Quelle méthode devrions-nous utiliser? Quelle qu’elle soit, la tâche sera considérable!!!
C’est ici que les carrés arithmétiques vont intervenir. Ceux-ci vont nous permettre de remplir la commande ci-haut d’une façon extrêmement simple!!! Vous les aurez vos 201 carrés magiques!!
11.2 Carrés arithmétiques d’ordre n
Considérons les n² expressions différentes suivantes :
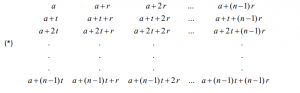
Celles-ci forment n suites arithmétiques de raison r (ce sont les n suites arithmétiques horizontales) et n suites arithmétiques de raison t (ce sont les n suites arithmétiques verticales). Le tableau (*) est appelé tableau arithmétique d’ordre n.
Ces n² expressions différentes ont donc la forme :
a + k1r + k2t
où k1 et k2 doivent prendre toutes les valeurs entières allant de 0 à n – 1 inclusivement.
Définition :

Le carré magique M ci-dessous est un carré arithmétique de somme 297; à sa droite, un tableau arithmétique correspondant.
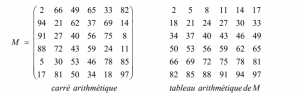
Les trente-six nombres de M se retrouvent dans un tableau arithmétique; nous y voyons les six suites arithmétiques horizontales de raison 3 et les six suites arithmétiques verticales de raison 16. Par contre, le carré magique suivant, un Dürer de somme 79, n’est pas un carré arithmétique. Nous verrons, plus bas, que cela est dû au fait que sa somme est un entier impair :
\(\begin{pmatrix} 5 & 4 & 19 & 51\\60 & 10 & 1 & 8\\2 & 15 & 53 & 9 \\12 & 50 & 6 & 11 \end{pmatrix}\)
[…]
